Jeg havde egentlig lukket min blog ned (manglende tid og for få besøgende til det var umagen værd at skrive nye indlæg), men her er lidt links til tidligre indlæg, som kan (lettere tilrettet) bruges til udendørs aktiviteter i disse Corona-tider.
Måske du kan blive inspireret af nogle af ideerne, når nu afgangseleverne vender tilbage til undervisningen.
Link til Pecha Kucha
Link til O-løb
Link til Goddag - ved du hvad?
Link til Hurtig walk and talk
Hvis du har spørgsmål til aktiviteterne må du gerne skrive til Jes S. Jørgensen.
Matematik i gymnasiet - på min måde...
I denne blog vil jeg skrive om den matematikundervisning, som jeg er tilhænger af.
torsdag den 16. april 2020
torsdag den 9. februar 2017
Differenttialligninger - tryghed og sikkerhed
Til den skriftlige eksamen på A-niveau er der jo typisk en opgave med differentialligninger. Når man retter sådanne opgaver, så ser jeg ofte, at eleverne ikke får løst differentialligningen pga. en eller anden dum indtastningsfejl.
Det har derfor været vigtigt for mig at træne eleverne i
1) at have et beredskab, hvis man ikke kan finde fejl i sin indtastning (eller hvis værktøjsprogrammet af en eller anden grund ikke kan løse ligning)
2) at finde fejl i egne indtastninger
Som afslutning på forløbet har eleverne derfor arbejdet med nogle opgaver, hvor de blev bedt om at løse differentialligningen med dsolve (Maple), formel fra formelsamling, separation af variable (hvis det er muligt).
Det gav eleverne en god træning i at have flere strategier ved opgaveløsningen. Separation af variable er selvfølgelig noget bøvlet, men omvendt kunne eleverne også se, at det var en stærk formel at råde over.
Eleverne arbejdede med dette ark: Link
Mht. træning i fejlsøgning lavede jeg en lille test i klassen, hvor eleverne fik udleveret 12 forskellige indtastninger af en differentialligning, som i alle tilfælde fejlede. Eleverne skulle så rette fejlene. Eleverne fik opgaverne udleveret i et Maple-dokument, så de direkte kunne rette fejlene til.
I dokumentet var det desuden meningen at eleverne skulle beskrive fejlen i ord. En opgave kunne f.eks. se således ud:
Det har derfor været vigtigt for mig at træne eleverne i
1) at have et beredskab, hvis man ikke kan finde fejl i sin indtastning (eller hvis værktøjsprogrammet af en eller anden grund ikke kan løse ligning)
2) at finde fejl i egne indtastninger
Som afslutning på forløbet har eleverne derfor arbejdet med nogle opgaver, hvor de blev bedt om at løse differentialligningen med dsolve (Maple), formel fra formelsamling, separation af variable (hvis det er muligt).
Det gav eleverne en god træning i at have flere strategier ved opgaveløsningen. Separation af variable er selvfølgelig noget bøvlet, men omvendt kunne eleverne også se, at det var en stærk formel at råde over.
Eleverne arbejdede med dette ark: Link
Mht. træning i fejlsøgning lavede jeg en lille test i klassen, hvor eleverne fik udleveret 12 forskellige indtastninger af en differentialligning, som i alle tilfælde fejlede. Eleverne skulle så rette fejlene. Eleverne fik opgaverne udleveret i et Maple-dokument, så de direkte kunne rette fejlene til.
I dokumentet var det desuden meningen at eleverne skulle beskrive fejlen i ord. En opgave kunne f.eks. se således ud:
søndag den 5. februar 2017
Gange to tal - sjov egenskab...
Jeg kan godt lide at give eleverne opgaver, hvor de selv skal komme med teorier/påstande, som vi så kan undersøge rigtigheden af.
En sådan lille opgave kunne f.eks. være:
1) Tegn f.eks. i Geogebra funktionen f(x)=x2.
2) Placer to punkter på parablen, hvor det ene skal have negativ x-værdi og det andet skal have positiv x-værdi. Vælg i første omgang hele tal som x-værdier.
3) Forbind de to punkter med en ret linje.
4) Hvilken sammenhæng er der mellem de to punkter på parablen og linjens skæring med y-aksen? Prøv forskellige ”pæne” punkter, som nedskrives i en tabel.
5) Kan du bevise din påstand? Start med udregning for to konkrete punkter og prøv så med x-værdierne x1 og x2.
En anden måske lidt sværere opgave er:
1) Afsæt 4 tilfældige punkter og forbind dem til en firkant.
2) Konstruer midtpunkterne på de 4 sider og forbind disse punkter til en ny firkant.
3) Hvad ser du? Er det altid sådan? Kan du bevise det?
En sådan lille opgave kunne f.eks. være:
1) Tegn f.eks. i Geogebra funktionen f(x)=x2.
2) Placer to punkter på parablen, hvor det ene skal have negativ x-værdi og det andet skal have positiv x-værdi. Vælg i første omgang hele tal som x-værdier.
3) Forbind de to punkter med en ret linje.
4) Hvilken sammenhæng er der mellem de to punkter på parablen og linjens skæring med y-aksen? Prøv forskellige ”pæne” punkter, som nedskrives i en tabel.
5) Kan du bevise din påstand? Start med udregning for to konkrete punkter og prøv så med x-værdierne x1 og x2.
En anden måske lidt sværere opgave er:
1) Afsæt 4 tilfældige punkter og forbind dem til en firkant.
2) Konstruer midtpunkterne på de 4 sider og forbind disse punkter til en ny firkant.
3) Hvad ser du? Er det altid sådan? Kan du bevise det?
onsdag den 28. december 2016
Repetition - med lidt bevægelse
Det har godt nok været sløjt med mine indlæg i efteråret 2016. Det er ikke nye ideer, som har manglet men snarere tid. Der har været mange andre gøremål. Her på falderebet til 2017 vil jeg præsentere en form for repetition, som jeg har lavet med min 3g-klasse.
Repetitionen handlede om vektorer i 2 dimensioner, men formen på øvelsen kan kopieres til andre former for repetition. I bunden af indlægget er der angivet et par andre ideer.
Efter en pause med vektorer var det tid til at få gennemgået vektorer i rummet, hvorfor det var naturligt at indlede med en repetition af vektorer i planen. Jeg fandt alle relevante formler frem (tak til formelsamlingen) og klippede dem ud, så der var en formel på hvert ark. Disse ark satte jeg op i et af vores fællesarealer.
Eleverne blev nu sat sammen i par, hvor hvert par blev udstyret med sedler i 3 forskellige farver. Jeg brugte grøn, gul og rød.
Farverne på sedlerne havde en betydning i relation til, hvad der skulle skrives på sedlen:
Grøn: Grafisk illustration af formlen (hvor det er muligt)
Gul: Sproglig beskrivelse af hvad formlen kan bruges til
Rød: Eksempel på opgave, hvor formlen kan benyttes.
Hvert par vælger nu en af de ophængte formler og udfylde en grøn, gul eller rød seddel. Sedlen hænges op ved siden af formlen med bagsiden udad, så det ikke kan ses, hvad der er skrevet på sedlen.
Parret går nu videre til en ny formel. Der skal være så mange formler at jeg kan kræve at der ikke må stå to par ved samme formel.
I første omgang må der ved hver formel kun hænge en rød, gul og grøn seddel. Så hvis man kommer til en formel, hvor der allerede hænger en grøn seddel, så skal parret vælge en rød eller gul seddel.
I og med at parrene har 2-3 sedler af hver farve, så kan man ikke nøjes med kun at lave f.eks. grafiske illustration. Det er først når et par har brugt alle deres sedler, at de kan få ekstra sedler af mig.
Kommer man til en formel, hvor der også hænger farvede sedler, så tales først om, hvad der mon står på sedlerne og efterfølgende tjekkes ved at vende sedlen. Herefter må parret udfylde en ny seddel.
Der kan evt. tillades flere sedler af samme farve, hvis der er flere muligheder ved en formel.
Da alle formler var blevet beskrevet, skulle parrene gennemgå alle formler, hvor det først skulle diskuteres, hvad der forventes at stå på de farvede sedler og efterfølgende tjekkes det, hvad der rent faktisk står på sedlerne.
Jeg forestiller mig at denne form for repetition f.eks. kan benyttes ved
- almindelig repetition af formler
- ved at angive forskrift for forskellige funktioner
- ved at angive grafer for forskellige funktioner
- ved eksamensopgaver, hvor man skal finde relevant formel
Eksempel med vektorformler.
- ...
Repetitionen handlede om vektorer i 2 dimensioner, men formen på øvelsen kan kopieres til andre former for repetition. I bunden af indlægget er der angivet et par andre ideer.
Efter en pause med vektorer var det tid til at få gennemgået vektorer i rummet, hvorfor det var naturligt at indlede med en repetition af vektorer i planen. Jeg fandt alle relevante formler frem (tak til formelsamlingen) og klippede dem ud, så der var en formel på hvert ark. Disse ark satte jeg op i et af vores fællesarealer.
Eleverne blev nu sat sammen i par, hvor hvert par blev udstyret med sedler i 3 forskellige farver. Jeg brugte grøn, gul og rød.
Farverne på sedlerne havde en betydning i relation til, hvad der skulle skrives på sedlen:
Grøn: Grafisk illustration af formlen (hvor det er muligt)
Gul: Sproglig beskrivelse af hvad formlen kan bruges til
Rød: Eksempel på opgave, hvor formlen kan benyttes.
Hvert par vælger nu en af de ophængte formler og udfylde en grøn, gul eller rød seddel. Sedlen hænges op ved siden af formlen med bagsiden udad, så det ikke kan ses, hvad der er skrevet på sedlen.
Parret går nu videre til en ny formel. Der skal være så mange formler at jeg kan kræve at der ikke må stå to par ved samme formel.
I første omgang må der ved hver formel kun hænge en rød, gul og grøn seddel. Så hvis man kommer til en formel, hvor der allerede hænger en grøn seddel, så skal parret vælge en rød eller gul seddel.
I og med at parrene har 2-3 sedler af hver farve, så kan man ikke nøjes med kun at lave f.eks. grafiske illustration. Det er først når et par har brugt alle deres sedler, at de kan få ekstra sedler af mig.
Kommer man til en formel, hvor der også hænger farvede sedler, så tales først om, hvad der mon står på sedlerne og efterfølgende tjekkes ved at vende sedlen. Herefter må parret udfylde en ny seddel.
Der kan evt. tillades flere sedler af samme farve, hvis der er flere muligheder ved en formel.
Da alle formler var blevet beskrevet, skulle parrene gennemgå alle formler, hvor det først skulle diskuteres, hvad der forventes at stå på de farvede sedler og efterfølgende tjekkes det, hvad der rent faktisk står på sedlerne.
Jeg forestiller mig at denne form for repetition f.eks. kan benyttes ved
- almindelig repetition af formler
- ved at angive forskrift for forskellige funktioner
- ved at angive grafer for forskellige funktioner
- ved eksamensopgaver, hvor man skal finde relevant formel
Eksempel med vektorformler.
- ...
torsdag den 3. november 2016
Arealet af enhedscirklen
Som afslutning på integralforløbet har mine 3g-ere i denne uge arbejdet med forskellige måder at bestemme areal på.
Hel konkret blev eleverne bedt om at udregne (en tilnærmelse til) arealet af enhedscirklen på forskellige måder.
Som lektie til første modul skulle eleverne komme med ideer til metoder, som kan benyttes til at bestemme enhedscirklens areal. De skulle både komme med forslag med og uden brug af hjælpemidler. Og de blev opfordret til at have integralregning i baghovedet.
I timen udvekslede eleverne deres ideer og forslagene blev præsenteret på tavlen. Der kom mange gode forslag.
Jeg havde på forhånd besluttet at fokusere på integralregning, så jeg tillod mig at forkaste geometriske metoder som f.eks. minder om Archimedes bestemmelse af pi.
Eleverne, som nu blev delt op i grupper, fik til opgave at skrive en lærebog om bestemmelse af arealet af enhedscirklen, hvor følgende beregningsmetoder skulle benyttes:
1) Brug af funktion med hjælp af Maple
2) Løsning i hånden ud fra stamfunktion fundet i gammel bog fyldt med stamfunktioner til alle mulige funktioner
3) Brug af summer
4) Brug af Taylorrækker
Vi har tidligere arbejdet med forberedelsesmaterialet om rækker og følger, så Taylorpolynomier er allerede kendte.
Delen med summer og Taylorrækker benyttes som minitræning frem mod SRP, idet eleverne selv skulle finde relevante materialer om summer (har ikke tidligere været gennemgået) og materialer til et lille teoriafsnit om Taylorrækker,. Materialerne skulle findes på nettet.
I den forbindelse benyttede jeg lejligheden til med eleverne, hvordan man gør den læste kilde til ens egen tekst og ikke bare skriver af fra kilden.
Vi diskuterede selvfølgelig også de forskellige løsningsmetoders styrker.
Jeg forventer, at dette projekt får en fremtrædende plads i et at mine spørgsmål til den mundtlige eksamen.
Du kan se den opgave eleverne fik udleveret efter deres brainstorm her.
Hel konkret blev eleverne bedt om at udregne (en tilnærmelse til) arealet af enhedscirklen på forskellige måder.
Som lektie til første modul skulle eleverne komme med ideer til metoder, som kan benyttes til at bestemme enhedscirklens areal. De skulle både komme med forslag med og uden brug af hjælpemidler. Og de blev opfordret til at have integralregning i baghovedet.
I timen udvekslede eleverne deres ideer og forslagene blev præsenteret på tavlen. Der kom mange gode forslag.
Jeg havde på forhånd besluttet at fokusere på integralregning, så jeg tillod mig at forkaste geometriske metoder som f.eks. minder om Archimedes bestemmelse af pi.
Eleverne, som nu blev delt op i grupper, fik til opgave at skrive en lærebog om bestemmelse af arealet af enhedscirklen, hvor følgende beregningsmetoder skulle benyttes:
1) Brug af funktion med hjælp af Maple
2) Løsning i hånden ud fra stamfunktion fundet i gammel bog fyldt med stamfunktioner til alle mulige funktioner
3) Brug af summer
4) Brug af Taylorrækker
Vi har tidligere arbejdet med forberedelsesmaterialet om rækker og følger, så Taylorpolynomier er allerede kendte.
Delen med summer og Taylorrækker benyttes som minitræning frem mod SRP, idet eleverne selv skulle finde relevante materialer om summer (har ikke tidligere været gennemgået) og materialer til et lille teoriafsnit om Taylorrækker,. Materialerne skulle findes på nettet.
I den forbindelse benyttede jeg lejligheden til med eleverne, hvordan man gør den læste kilde til ens egen tekst og ikke bare skriver af fra kilden.
Vi diskuterede selvfølgelig også de forskellige løsningsmetoders styrker.
Jeg forventer, at dette projekt får en fremtrædende plads i et at mine spørgsmål til den mundtlige eksamen.
Du kan se den opgave eleverne fik udleveret efter deres brainstorm her.
lørdag den 15. oktober 2016
Induktion - differentiation og legoklodser
I forbindelse med differentialregning, så benytter jeg differentiation af xn til at introducere bevis med induktion for mine elever.
Vi kigger på små forskellige sætninger, som kan bevises med induktionsprincippet:
1) Vinkelsummen i en n-kant
2) Summen af tallene fra 1 til n
3)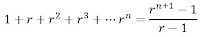
Vi vil også "lege" lidt med fysiske legoklodser, idet eleverne skal kigge på kvadrater, som bygges ud fra kvadratiske klodser på formen
Ideen til opgaven har jeg fået fra bogen "Fagdidaktik i matematik" af Morten Blomhøj, som er udgivet på forlaget Frydenlund i 2016, hvor det bl.a. diskuteres, hvordan man også kan arbejde med problemet i folkeskolen.
Mit arbejdsark til lego-opgaven finder du her.
De indledende øvelser mht. differentiation af xn er vedhæftet her.
Vi kigger på små forskellige sætninger, som kan bevises med induktionsprincippet:
1) Vinkelsummen i en n-kant
2) Summen af tallene fra 1 til n
3)
Vi vil også "lege" lidt med fysiske legoklodser, idet eleverne skal kigge på kvadrater, som bygges ud fra kvadratiske klodser på formen
Eleverne skal nu når de bygger kvadraterne udfylde nedenstående skema (Bredde er antal klodser på kantsiden)
I sidste linje skal eleverne opstille formler hørende til kolonneoverskriften, og det er så meningen, at eleverne skal bevise udvalgte formler.
Opgaven indeholder som det ses også en træning i at opstille funktionsudtryk, så man kan evt. nøjes med at opstille funktionsforskrifterne uden at bevise påstandene formelt ved hjælp af induktion.Ideen til opgaven har jeg fået fra bogen "Fagdidaktik i matematik" af Morten Blomhøj, som er udgivet på forlaget Frydenlund i 2016, hvor det bl.a. diskuteres, hvordan man også kan arbejde med problemet i folkeskolen.
Mit arbejdsark til lego-opgaven finder du her.
De indledende øvelser mht. differentiation af xn er vedhæftet her.
mandag den 29. august 2016
Hjemmeopgaver - Ikke kun en løsningsmetode og tjek af løsning
Eleverne skal have et beredskab, de kan benytte, hvis de har problemer med at løse en opgave. Problemet kan skyldes, at de ikke kan finde ud af at løse opgaven eller at matematikprogrammet driller.
Jeg gør en del ud af at træne forskellige løsningstyper, så eleverne ikke altid er bundet til en bestemt løsningsmetode.
Det er selvfølgelig ikke altid, det er muligt at konstruere en alternativ løsning, der giver fuldt point, men få point er bedre end ingen.
De stærke matematikelever får også noget ud at arbejdet med alternative løsningsmetoder, da disse kan benyttes som tjek.
Når eleverne har arbejdet med forskellige løsningsstrategier, så oplever jeg, at eleverne i fremtidige besvarelser vælger forskellige metoder. Eleverne er altså ikke enige om, hvilke metoder de foretrækker. Det gør det også vigtigt, at vise forskellige strategier og metoder, da det er med til at stille den enkelte elev bedre til eksamen.
Mine elever afleverer i denne uge bl.a. følgende opgave - inspireret af en tidligere eksamensopgave:
Jeg gør en del ud af at træne forskellige løsningstyper, så eleverne ikke altid er bundet til en bestemt løsningsmetode.
Det er selvfølgelig ikke altid, det er muligt at konstruere en alternativ løsning, der giver fuldt point, men få point er bedre end ingen.
De stærke matematikelever får også noget ud at arbejdet med alternative løsningsmetoder, da disse kan benyttes som tjek.
Når eleverne har arbejdet med forskellige løsningsstrategier, så oplever jeg, at eleverne i fremtidige besvarelser vælger forskellige metoder. Eleverne er altså ikke enige om, hvilke metoder de foretrækker. Det gør det også vigtigt, at vise forskellige strategier og metoder, da det er med til at stille den enkelte elev bedre til eksamen.
Mine elever afleverer i denne uge bl.a. følgende opgave - inspireret af en tidligere eksamensopgave:
Det er et krav, at opgaven løses i Maple.
I næste uge skal eleverne aflevere samme opgave, men denne gang skal løsningerne bestemmes i Geogebra.
Det er svært at få hele dokumentationen og centrale kommentarer med ved løsning af opgaver i Geogebra . Derfor får eleverne følgende huskeregler til løsning af opgaver med Geogebra:
Det er svært at få vænnet eleverne til at tjekke om resultatet på et spørgsmål er rimeligt/korrekt. Jeg vil derfor inden længe give eleverne en hjemmeopgave, hvor svarene er angivet.
Eleverne skal så i stedet for at løse opgaverne tjekke om svarene er korrekte - det vil de selvfølgelig ikke være alle sammen.
Abonner på:
Opslag (Atom)








